Line Tangent to a Curve

Posted on June 3, 2012 by Alex Nelson

1. Overview. Suppose we have a line {\ell} in the plane {{\mathbb R}^{2}}. What data do we need to specify a line?

We need a slope {m} and a point {(x_{0}, y_{0})} on the line {\ell}. Then we can specify {\ell} completely by the equation
(1)\displaystyle \frac{y-y_{0}}{x-x_{0}}=m.
We can rewrite this as
(2)\displaystyle y = y_{0} + m(x-x_{0}).
Lets remember this.

Last time we discussed the derivative, and the derivative gives us the slope at a point {(x,f(x))}. But look: we have the slope from the derivative.

What more information do we need to compute a line? We need a point on the curve! So if {y=f(x)} is a curve, and {(x_{0},y_{0}=f(x_{0}))} is a point on the curve, then we can compute the line tangent to {y} at {x_{0}} as
(3)\displaystyle t_{y_{0}}(x) = y_{0} + \left.\frac{\mathrm{d} f}{\mathrm{d} x}\right|_{x=x_{0}}\cdot(x-x_{0})
This uses the derivative {f'(x_{0})} as the slope, and the data {(x_{0}, y_{0})}.

(We should quickly prove to ourselves this passes through the desired point. It is a one minute check that t_{y_{0}}(x_{0}) = y_{0}+0. We also see it has the desired slope, and it is in fact a line.)

Lets now consider a few examples.

2. Basic Algorithm. So, what’s the basic algorithm when finding the tangent line of the curve y=f(x) at the point (x_{0}, y_{0})?

Step 1. Find the derivative f'(x).
Step 2. Using Step 1’s results, evaluate the derivative at x_{0}, i.e., evaluate f'(x_{0}).
Step 3. Using Step 2’s results, plug it into the formula t(x)=y_{0}+f'(x_{0})\cdot(x-x_{0}).

We will do each step and draw the doodles as we go.

Example 1. Lets find the tangent line passing through the point (1,2) for the curve y=f(x)=x^{2}+1. What to do?

Step 0: draw the curve. We will doodle the curve in blue, just so we understand which part of the graph is the curve.

Step 1: find the derivative f'(x). We see that the derivative for x^{2}+1 is, well, by using linearity
\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}(x^{2}+1)=\frac{\mathrm{d}(x^{2}}{\mathrm{d}x}+\frac{\mathrm{d}(1)}{\mathrm{d}x}
Then we invoke the power rule to find
\displaystyle\frac{\mathrm{d}(x^{2}}{\mathrm{d}x}+\frac{\mathrm{d}(1)}{\mathrm{d}x}=2x + 0
Thus we find
\displaystyle f'(x)=2x
This concludes step 1.

Step 2: Evaluate f'(x_{0}). OK, so we just found f'(x)=2x and we have x_{0}=1. Thus we find
\displaystyle f'(1)=2
This concludes step 2.

Step 3: Construct Tangent Line. Well, we have the formula for the tangent line be
\displaystyle t(x)=y_{0}+f'(x_{0})\cdot(x-x_{0})
We have everything we need. We plug in y_{0}=2 and x_{0}=1, and results from step 2, to get
\displaystyle t(x)=2+2\cdot(x-1)
But we may simplify things out:
\displaystyle t(x)=2+2x-2=2x
Thus the tangent to f(x)=x^{2}+1 at (1,2) is
\displaystyle t(x)=2x
We can doodle this:

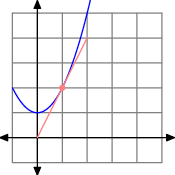
Note the curve is doodled in blue, the tangent point is emphasized, and the tangent line is doodled in pink.

Conclusion.
We will conclude this post with motivation for the next:

Problem. We want to find some curve {y=f(x)} such that at any point {(x_0,y_0)} on the curve its tangent line {t_{y_{0}}} satisfies the property {t_{y_{0}}(x_{0}-1)=0}. What is {y=f(x)}?

(The field called “Differential Equations” studies this general sort of problem “Find the curve whose derivative satisfies…”)

About Alex Nelson

I like math. I like programming. Most of all, I love puzzles.
This entry was posted in Calculus, Differential, Tangent Line. Bookmark the permalink.

5 Responses to Line Tangent to a Curve

  1. Pingback: Exponential Function | My Math Blog

  2. Pingback: Tangent Lines as Linear Approximations | My Math Blog

  3. Pingback: Optimization (Motivation) | My Math Blog

  4. Pingback: [Index] Calculus of a Single Variable | My Math Blog

  5. Pingback: [Index] Calculus in a Single Variable | My Math Blog

Leave a comment